PCR検査をどんどん増やすべきか?…「不完全情報のワナ」(1) |
新型コロナウイルス禍で緊急事態宣言が出されて以来、自粛して家にいるとTVやネットを見る時間が増え、近所の速足散歩以外は日がな一日コロナ関連の情報に接します。その中で気になったのは、色々な人達が外野から好き勝手に、当事者である医療関係者や政府・自治体の政策立案者・実務者の行動を批判している態度、というか「外野からの騒音」でした。 そんな観点で色々と見聞きしている中で、以下のURL①の、神奈川県医師会菊岡会長の「市民の皆様へ」というコメントに出会いました。外野ではない現場の第一線で働く当事者の方々の悲痛な生の声を聞いて胸を打たれました。 これを読んで、かつてスタンフォード大学で学んだ意思決定論の授業で出てきた「ベイズ推定」というアプローチを思い出しました。精度が100%でない検査なり調査結果をどう解釈し、意思決定に活用するかという文脈で学んだのですが、ベイズという牧師が提唱し、後に数学者のラプラスらが定式化した「ベイズの定理」というのを使います。 授業でベイズ推定の考え方に初めて接した時、脳裡に、標題に掲げた「不完全情報のワナ/トラップ/落とし穴」という言葉が浮かんだのを思い出したのです。その時の「え?本当にそうなの?」というある種の「だまされた感/意外感」や、その後に思った「なるほど、そうなんだ!」感の印象が強く、今回のPCR検査のケースにあてはめて考えるのが有効ではないかと思った訳です。 もう一言付け加えると、今聞こえてくる色々な声を聞いていると、PCR検査を増やすべきか否かについて、定性的&情緒的なものが多く、定量的な議論が非常に少ない印象を持ちます。やはり議論は、ゼロかイチかの定性的なものにとどまらず、定量的に行わないと冷静な論理的なものにならないと思います。その意味で、ここからの検討は、少し面倒と感じられる部分もあるかと思いますが定量的なロジックで一歩一歩進めていきますので、辛抱強くお付き合いください。 具体的には、菊岡会長をはじめとする医療現場の立場から、 「PCR検査の対象をほとんど絞らず、感染している可能性が低い人たちも含む希望者全員に対して行うといったいどうなるのか? 医療崩壊で大勢の死者が出てしまう危険性の防止のために検査対象を絞り込むことは本当に是なのか?」 という問いを検証する、というフレームです。 別の言い方をすれば、「医療現場的」世界観、ないしPCR検査のプロセスやプロトコルを設定する「医療政策現場的」世界観での検討フレーム、ということです。 このフレーム設定のもとでの検討に進む前に、まず第一歩として、PCR検査の「臨床試験研究的」場面を想定します。 この「臨床試験研究的」場面では、あらかじめ罹患している確率(潜在罹患率)がわかっている検査対象集団を設定し、その中の一人に対してこれからPCR検査をしたときに、その人が罹患しているか否かがどの程度正確に検出されるか、それがPCR検査の精度として示されることになります。 この状況を次のように叙述することにします。 この場合を使って、スタンフォード大学でハワード教授から習った、ディシジョンツリーを使ったベイス推定のやり方を説明します。(この場合、意思決定項目がないので、厳密にはディシジョンツリーでなく、Probability Tree=プラバビリティ(確率)ツリーですが、簡便性のためご容赦ください。) URL②:https://qiita.com/oki_mebarun/items/ee345ba45c7d3752b54c 想定した「臨床試験研究的」場面でのPCR検査の状況をディシジョンツリーの形で示したのが図1-1です。 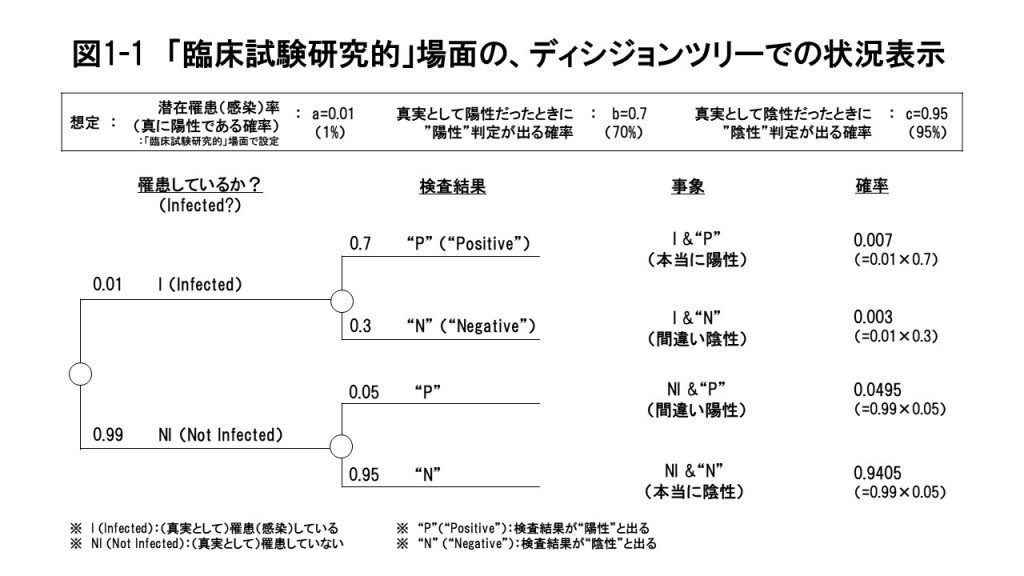 図1-1の左側から順番に説明していきましょう。まず検査前において、目の前の検査対象者が実際に(真実として)新型コロナウイルスに罹患(=感染)しているかどうかは不確実です。この人物は潜在罹患率a=0.01の検査対象集団の中の一人なのですが、当人が実際に感染しているか否かはわかっていない状況だということです。 従って不確実性としては、この人が罹患しているか(I:Infected)/罹患していないか(NI:Not Infected)の2つのシナリオがあります。不確実性を示す小さい〇から2つのシナリオ(I or NI)の枝が分かれて出て行って、潜在罹患率a=0.01を反映して、それぞれの確率が0.01と0.99となることを、一番左側のツリーは示しています。 次にIとNIそれぞれの枝から、検査結果の “P”(Positive:”陽性”)と“N”(Negative:”陰性”)が枝分かれします。結果的には左から2列目は4つの枝として示され、それぞれの起こる確率が、b=0.7とc=0.95を反映して、上から順に0.7/0.3、0.05/0.95と示されています。 左から3つ目の列には「事象」とありますが、これは4つの枝分かれ(=シナリオ)の状況を記述したものです。 上から順に 罹患していて検査結果が “陽性” と出るシナリオ(I & “P”:本当に陽性)、 罹患しているが検査結果は “陰性” と出るシナリオ(I &“N”:間違い陰性)、 罹患していないが検査結果は “陽性” と出るシナリオ(NI & “P”:間違い陽性)、 罹患しておらず検査結果も“陰性”と出るシナリオ(NI & “N”:本当に陰性) となっています。 その次の左から4つ目の列は「確率」で、それぞれの4つのシナリオがどれくらいの確率で起こるかを示しています。例えば、一番上のI & “P” のシナリオは、Iの確率0.01と そのシナリオでの“P” の確率0.7を掛け合わせて0.007、その下のI &“N” は、0.01×0.3=0.003という具合です。同様にして、NI & “P” と NI & “N” のシナリオの確率も計算して記しています(それぞれ0.0495と0.9405)。 図1-1で、もしb=1、c=1、つまりPCR検査の精度が完ぺき(100%)だとしたら、目の前の人が真実として罹患していれば検査結果も必ず”陽性”と出るし、逆に真実として罹患していなければ検査結果も必ず”陰性”と出ます。そしてこの場合、ここからが大事なのですが、検査結果が”陽性”と出ればその人は真実として罹患しているし、”陰性”と出れば真実として罹患していないわけです。 しかし実際には検査精度が100%でないがゆえに、検査結果が”陽性”と出ても本当は陰性の人がいるし、検査結果が”陰性”と出ても真実としては罹患していない人が一定の割合で出てくる、ということです。「PCR検査を何が何でもどんどん増やせ!」という論調の人たちの話を聞いていると、この検査精度の不完全さを失念しているのではないかと強く感じられます。 さてここまでは図1-1を参照しながら、検査対象集団の潜在罹患率aがわかっている状況で、PCR検査の精度であるb、cに照らすと、ある一人の人に対して検査をしたときに、どんな状況がどんな確率で起こりうるか、という「臨床試験研究的」場面を叙述してきましたが、ここからいよいよ実際の「医療現場的」場面の話に移っていきます。 この医療現場的場面では、検査対象集団の潜在罹患率aについては、PCR検査のプロトコルや診断基準(=医療プロトコル)をあらかじめ設定することで調整できることを想定しています。 当然のことながら、「熱も咳もないけど何となく心配だから検査してほしい、というような人も全員希望者を受け入れる」というプロトコルと、「平熱より1.5度以上体温が高い日が2日間以上続き、かかりつけ医の診断を通じて咳と倦怠感や痛みその他の症状が一定以上の深刻さを伴うと判断される人たちだけに絞りこむ」というプロトコルでは、検査対象集団の潜在罹患率は大きく異なるはずです。そしてそのあたりに関する専門家の知見を総動員すれば、検査対象集団の潜在罹患率の調整は可能、という想定に立っています。 そうして潜在罹患率がaに調整された検査集団の中のある一人に対してPCR検査を行い、検査結果が”P”ないし”N” と出た時に、その「検査結果」という新たな情報を知ったうえで、果たしてその人が本当にIなのか(罹患しているか)NI(罹患していない)なのかを、あらかじめ臨床試験研究的場面で確認してあるbとcの値を使って推定する必要があるのが、「医療現場的」場面なのです。 まさにこの、検査結果が出た(わかった)上で、その人が本当に罹患しているかいないかを推定するのが、ベイズ定理を使った「ツリーフリッピング」つまりツリーのひっくり返しという操作です。
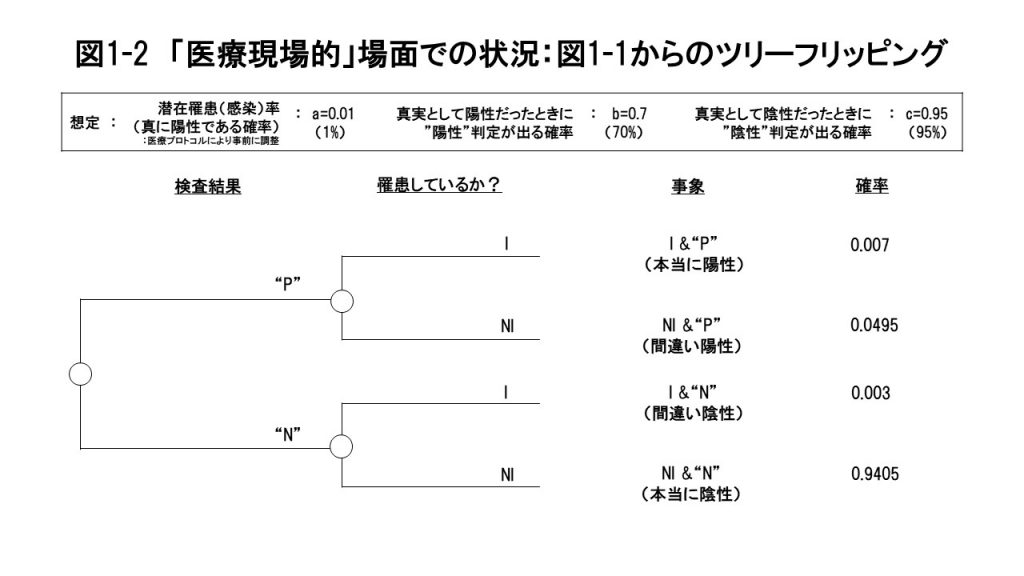 まず医療現場では、最初に検査結果 “P” か “N” の情報がもたらされます。そしてその次に、“P” か “N”かという新たな情報がわかったうえで、目の前の検査対象者が実際に罹患しているかいないかの確率を推定することになります。(この推定を「ベイズの定理」に基づいた推定、という意味で「ベイズ推定」と呼ぶわけです。) ここからがいよいよベイズ推定の核心部分で、図1-2の情報から順次、検査結果である“P”/“N” の確率と、“P” と出た場合に実際に I である確率、そして、“N” と出た場合に、本当にN I である確率等を計算していきます。 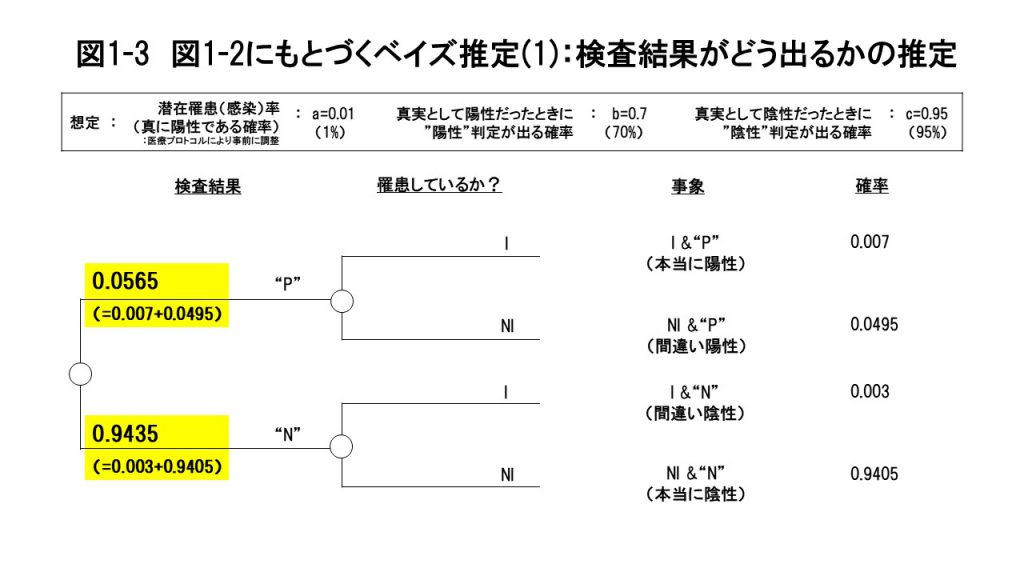 図1-3を見てください。まず検査結果が “陽性”(“P”)と出る確率は、それを構成する2つのシナリオ( I &“P”と NI & “P” )、つまり、実際に陽性で検査でも“陽性”と出るシナリオ(本当に陽性)と、実際には陰性なのに検査精度の問題で“陽性”と出るシナリオ(間違い陽性)の2つの場合の合計の確率ということで、0.007+0.0495=0.0565となります。 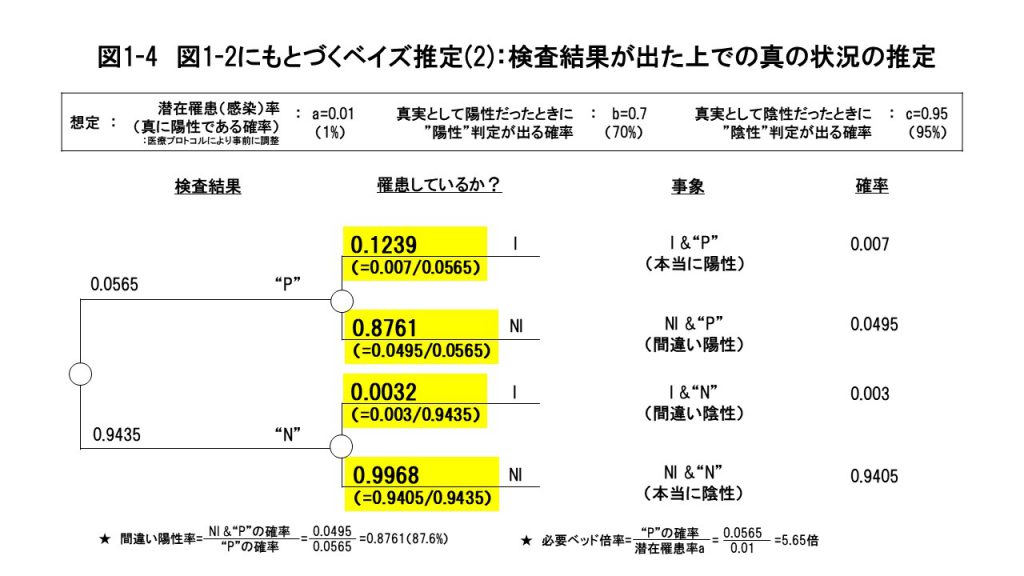 まず検査結果が “P”と出た場合、本当に陽性である確率は、“P” になったシナリオにおいて、どれだけの確率で I &“P” になるかということのはずなので、I &“P” の確率の0.007を “P” となる確率0.0565で割って、0.1239(=0.007/0.0565)、 となります。 以上の、検査結果が”P”と出たうえでの、2つのシナリオ(「本当に陽性」と「間違い陽性」)の確率の合計は、当然のことながら1(=0.1239+0.8761)となることを確認してください。 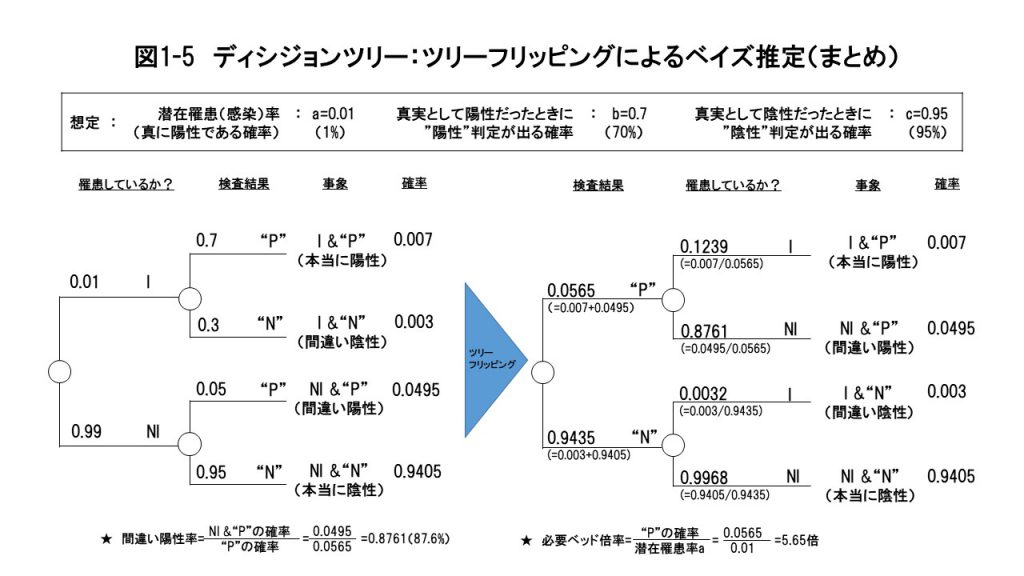 さてここから、ここまでの分析から、どんな洞察が導き出されるか考えていきます。 そこで本来は必要のない、間違い陽性の人達のための無駄なベッドも含めたベッド数を、真に必要なベッド数に対する割合として「必要ベッド倍率」と定義して計算してみます。必要ベッド倍率は、医療資源の無駄遣いの度合いを示す指標になります。具体的には、“P” の確率0.0565を、検査集団全体の真の罹患率である潜在罹患率(=0.01)で割って、5.65倍となります。相当大きいですよね。 さらにもう一つ、a=0.01のような潜在罹患率が低い状況では「間違い陰性」が出る確率が極めて小さいこと、すなわち罹患していない人の割り出しがかなり正確にできることの意味合いを考えてみます。具体的には、この利点を活用し、世の中で最も感染を防止しなければならないタイプの人たち—医療関係者や物流、小売りの現場等々、社会の基幹インフラを支える人たち—へのPCR検査を優先的に行うことの有効性です。 こういった人たちに対しては、少しでも心配なことがあれば、すぐにもPCR検査を実施して陰性であることを確認する。もし”陽性”と出た場合には隔離することで、社会の基幹インフラを担う人たちの間での感染を防ぎ、社会機能のマヒ・崩壊を未然に防ぐのです。(もし”陽性”と出た場合には、間違い陽性の可能性を考えて、確認のための追加検査は必要だと思います。) そういった人たちに優先的にPCR検査の医療資源を振り向けるためにも、むやみに(希望者全員に対してといった勢いで)PCR検査を行うことは慎むべきだということです。
。。。とここまでお話ししてきたところで、ブログ記事としてはかなり長くなってしまいましたので、続きは次のブログ【PCR検査をどんどん増やすべきか?…「不完全情報のワナ」(2)】でご説明したいと思います。 ☆今回のブログ記事の中には、私が医療分野の専門家ではないが故の不正確な記述等が含まれている可能性がありますが、その点は何卒あらかじめご了承ください。 |
|
コメント
|


